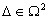Родионов В.И. (Ижевск УдГУ)

Вложение импульсных систем в семейство квазиинтегральных уравнений

Если Q ≈ непрерывная функция ограниченной вариации, то все непродолжаемые решения однопараметрического семейства квазиинтегральных уравнений (с параметром )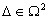

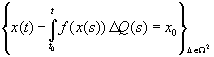(1)

совпадают между собой и с непродолжаемым решением интегрального уравнения 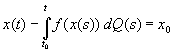. В более общей ситуации, когда Q имеет разрывы, вводится понятие аппроксимируемого решения и доказывается, что семейство (1) имеет единственное непродолжаемое аппроксимируемое решение. Приводится алгоритм построения этого решения.