Семинар Отдела динамических систем
Выделение ядер выживаемости и инвариантности
для дифференциального включения,
функционирующего на конечном промежутке времени
при наличии нестационарного фазового ограничения.
В.Н. Ушаков, А.Б. Заварин
Доклад посвящен решению задачи выживания дифференциального включения в нестационарных фазовых ограничениях. Тематика доклада примыкает к работам
[1-5].
В докладе рассматривается управляемая система
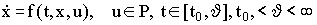 (1)
(1)
Здесь
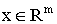 - фазовый вектор системы
- фазовый вектор системы 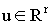 , - управление,
, - управление, 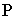 - компакт в евклидовом пространстве
- компакт в евклидовом пространстве 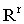 . Предполагается, что выполнены условия:
. Предполагается, что выполнены условия:
- Вектор-функция
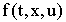 непрерывна по
непрерывна по 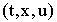 в множестве
в множестве 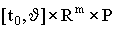 и локально липшицева по
и локально липшицева по 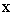
- Существует такая константа
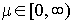 , что
, что 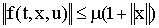
Рассматривается дифференциальное включение (д.в.)
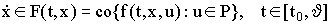 (2)
(2)
соответствующее системе (1). Предполагается, что наряду с (1) и (2) задано замкнутое множество
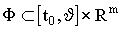 , имеющее непустые сечения
, имеющее непустые сечения 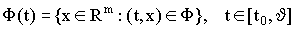 , причем
, причем 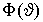 - компакт в
- компакт в 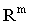 .
.
Предлагаются попятные алгоритмы приближенного построения ядра выживаемости
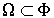 и ядра инвариантности
и ядра инвариантности 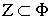 д.в. (2) в множестве
д.в. (2) в множестве 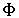 . А именно, определяется система
. А именно, определяется система 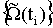 множеств
множеств 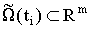 , отвечающая конечному разбиению
, отвечающая конечному разбиению 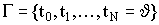 отрезка
отрезка 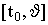 :
: 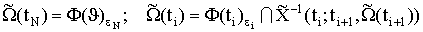 , где
, где 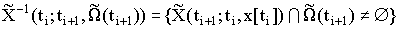 ,
, 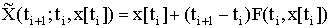 ,
, 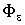 -
- 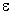 -окрестность множества
-окрестность множества 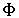 , последовательность
, последовательность 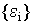 определяется рекуррентными соотношениями
определяется рекуррентными соотношениями 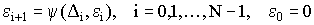 и удовлетворяет равенству
и удовлетворяет равенству 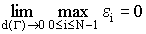 ,
, 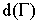 -диаметр разбиения
-диаметр разбиения 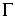 .
.
Вводится в рассмотрение множество
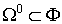 как некоторый предел системы множеств
как некоторый предел системы множеств 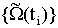 при диаметре разбиения
при диаметре разбиения 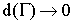 .
.
Доказывается утверждение
Т е о р е м а 1
. 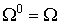 .
.
Аналогичный подход применяется в отношении ядра
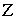 инвариантности д.в. (2) в множестве
инвариантности д.в. (2) в множестве 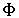 .
.
Предлагается также алгоритм построения
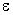 -выживающих решений управляемой системы (1) и д.в. (2).
-выживающих решений управляемой системы (1) и д.в. (2).
Л и т е р а т у р а
- Красовский Н.Н., Субботин А.И. Позиционные дифференциальные игры. М.: Наука, 1979.
- A.B. Kurzhanski and T.F. Filippova. On the Trajectory Tubes - A Mathematical Formalizm for Uncertain Dynamics, Viability and Control. Advances in Nonlinear Dynamics and Control: A Report from Russia, 1993, Birkhauser, pp. 122-188.
- J.-P. Aubin. Viability theory. Birkhauser, 1992.
- В.Н. Ушаков. К задаче построения стабильных мостов в дифференциальной игре сближения-уклонения. Изв. АН СССР. Техн. кибернетика.
N 4, 1980. С. 32-45
- В.Н. Ушаков, А.П.Хрипунов. О приближенном построении решений в игровых задачах управления. прикладная математика и механика. Т. 61, вып. 3, 1997. С. 413-421.
![]() (1)
(1)![]() (2)
(2)