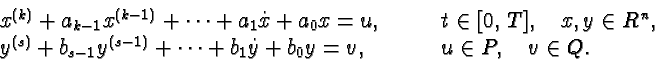 |
(1) |
Семинар Отдела динамических систем,
9 февраля 2000 г., 1430
Обобщенным контрольным примером Л.С.Понтрягина в теории
дифференциальных игр называют задачи, где динамика движения двух
управляемых объектов описывается линейными дифференциальными
уравнениями
В эквивалентных координатах игра (1) принимает
размерность ![]() по фазовой переменной.
по фазовой переменной.
Если множества ![]() и
и ![]() -- шары с центром в начале координат, то
-- шары с центром в начале координат, то
![]() -сечения множеств уровня функции цены (максимальных стабильных
мостов) также будут шарами с центром в начале координат.
Зависимость радиуса от времени может быть получена
аналитически, либо при помощи несложного численного
интегрирования. Фактически, в данном случае имеем дело с
эквивалентной фазовой переменной размерности 1. Поэтому данный
случай не представляет интереса с точки зрения построения
множеств уровня функции цены.
-сечения множеств уровня функции цены (максимальных стабильных
мостов) также будут шарами с центром в начале координат.
Зависимость радиуса от времени может быть получена
аналитически, либо при помощи несложного численного
интегрирования. Фактически, в данном случае имеем дело с
эквивалентной фазовой переменной размерности 1. Поэтому данный
случай не представляет интереса с точки зрения построения
множеств уровня функции цены.
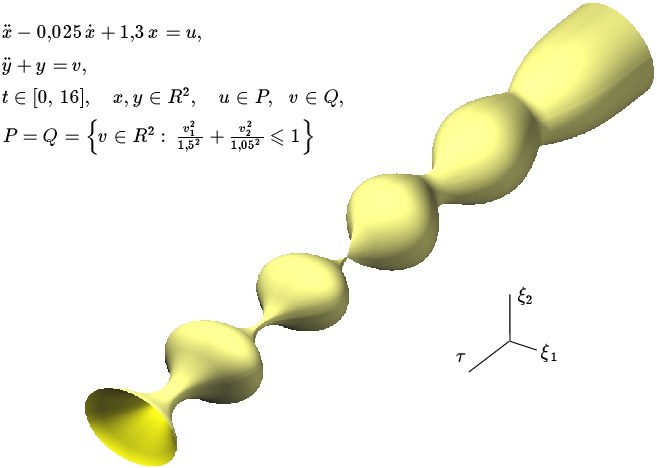
В докладе рассматриваются задачи, где ![]() , а множества
, а множества ![]() и
и ![]() являются эллипсами. Исследуются ситуации, когда множества уровня
функции цены в пространстве
являются эллипсами. Исследуются ситуации, когда множества уровня
функции цены в пространстве
![]() имеют узкие шейки.
Здесь
имеют узкие шейки.
Здесь
![]() -- эквивалентные координаты. На рисунке
показан пример множества уровня с двумя узкими шейками.
Символ
-- эквивалентные координаты. На рисунке
показан пример множества уровня с двумя узкими шейками.
Символ ![]() обозначает обратное время.
обозначает обратное время.